Binary trees are one of the most used data structures in programming.
Binary search trees allow efficient traversal, search, deletion, and insertion operations.
Since it processes nodes in ascending value order, the technique is called inorder traversal.

Traversing is the process of visiting each node in a tree data structure exactly once.
For the subtree 32, first traverse the left subtree, 28.
This subtree doesn’t have any children, so next traverse the 32 node.
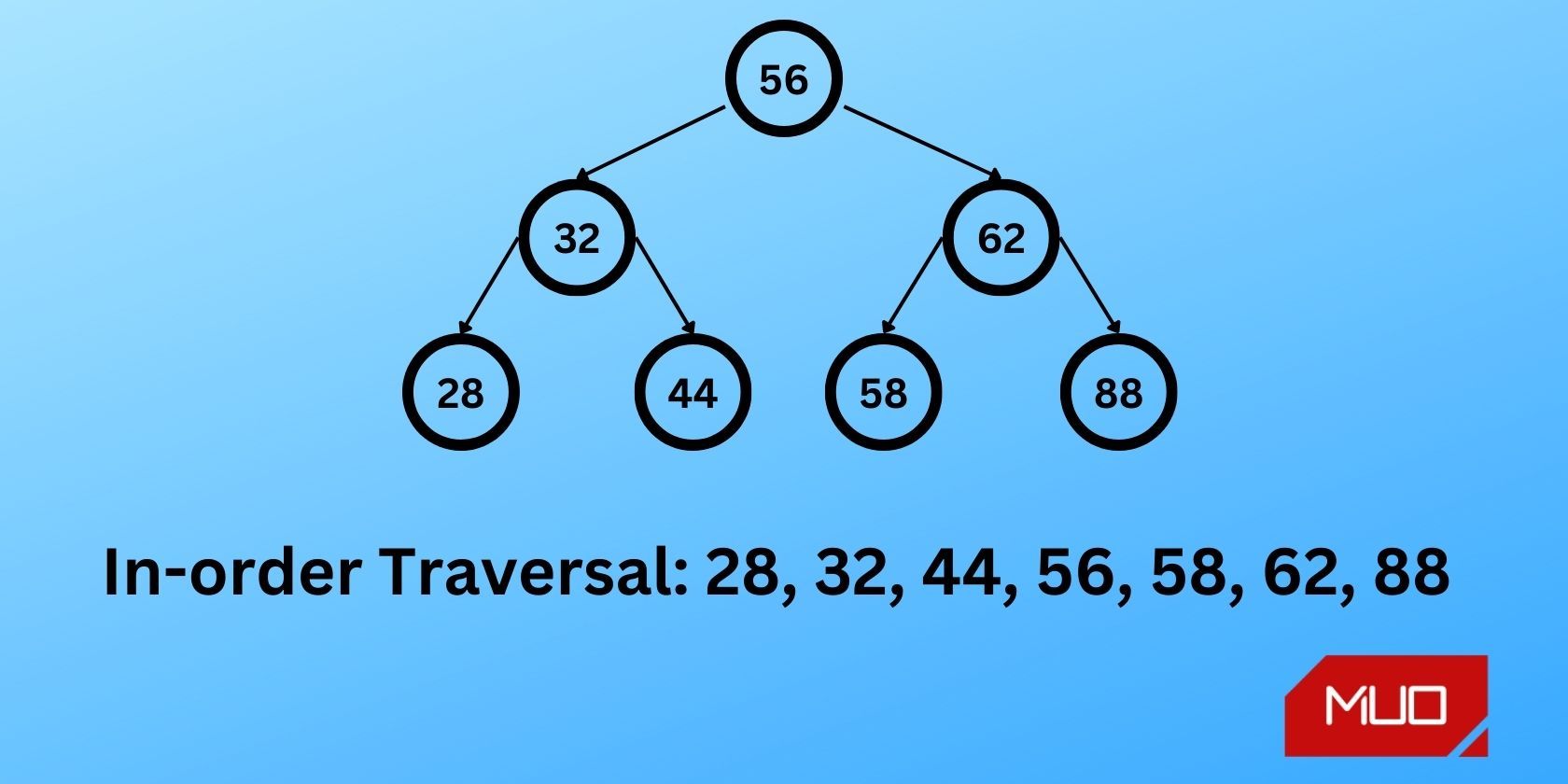
Next, traverse the right subtree, 44, which also has no children.
Therefore the order of traversal for the subtree rooted at 32 is 28 -> 32 -> 44.
Next, visit the root node, 56.
Then, traverse the right subtree, rooted at 62.
Start by traversing its left subtree, rooted at 58.
It doesn’t have any children, so visit the 62 node next.
Finally, traverse the right subtree, 88, which also has no children.
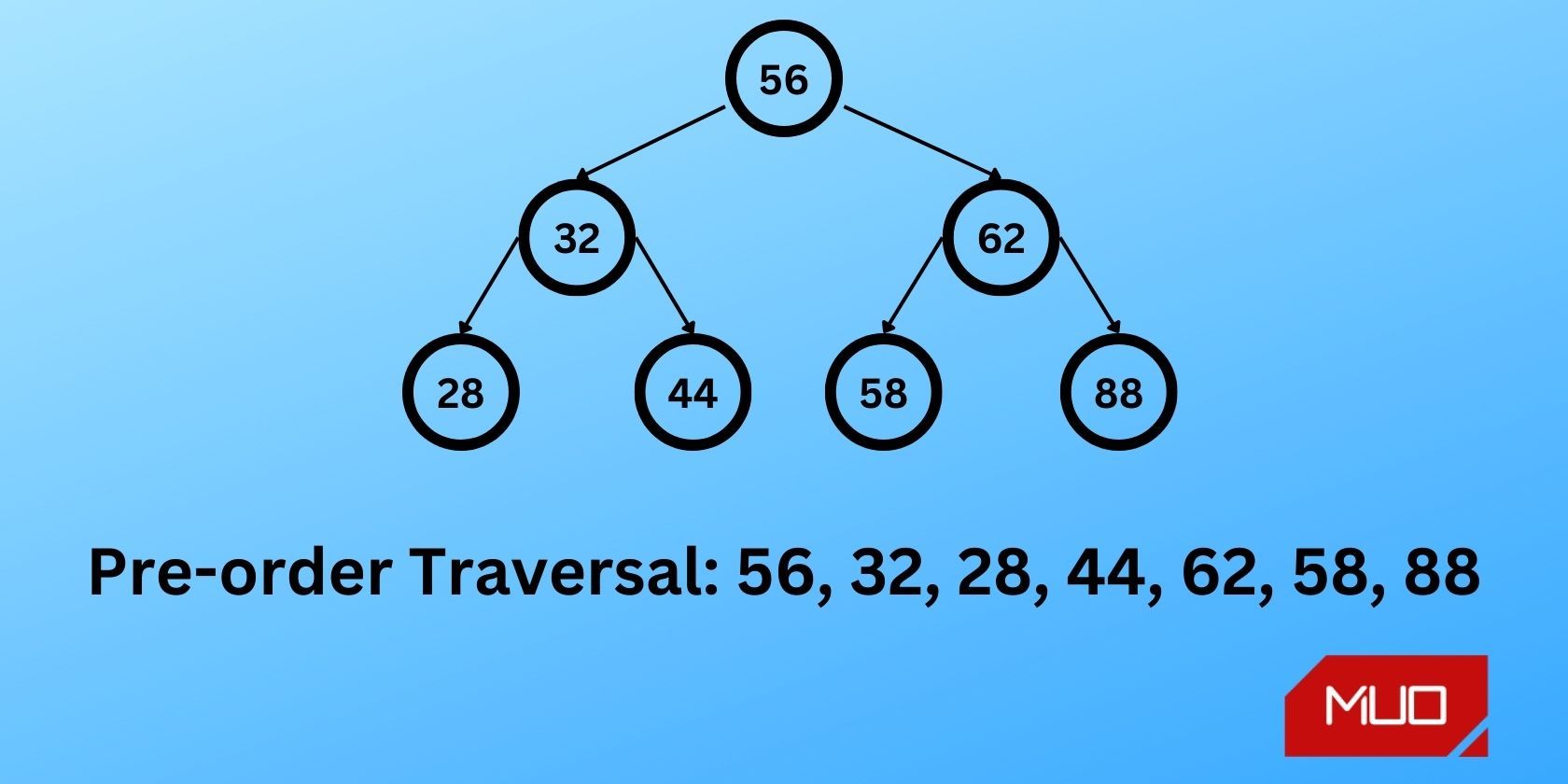
you’re able to use the algorithm to find the prefix expression of an expression tree.
Then traverse the left subtree, 32, followed by the right subtree, 62.
For the left subtree, process the value at the root node, 32.
Next, traverse the left subtree, 28, then finally the right subtree, 44.
This completes traversal of the left subtree rooted at 32.
The traversal occurs in the following order: 56 -> 32 -> 28 -> 44.
For the right subtree, process the value at the root node, 62.
Next, traverse the left subtree, 58, then finally the right subtree, 88.
Again, neither node has any children, so traversal is complete at this point.
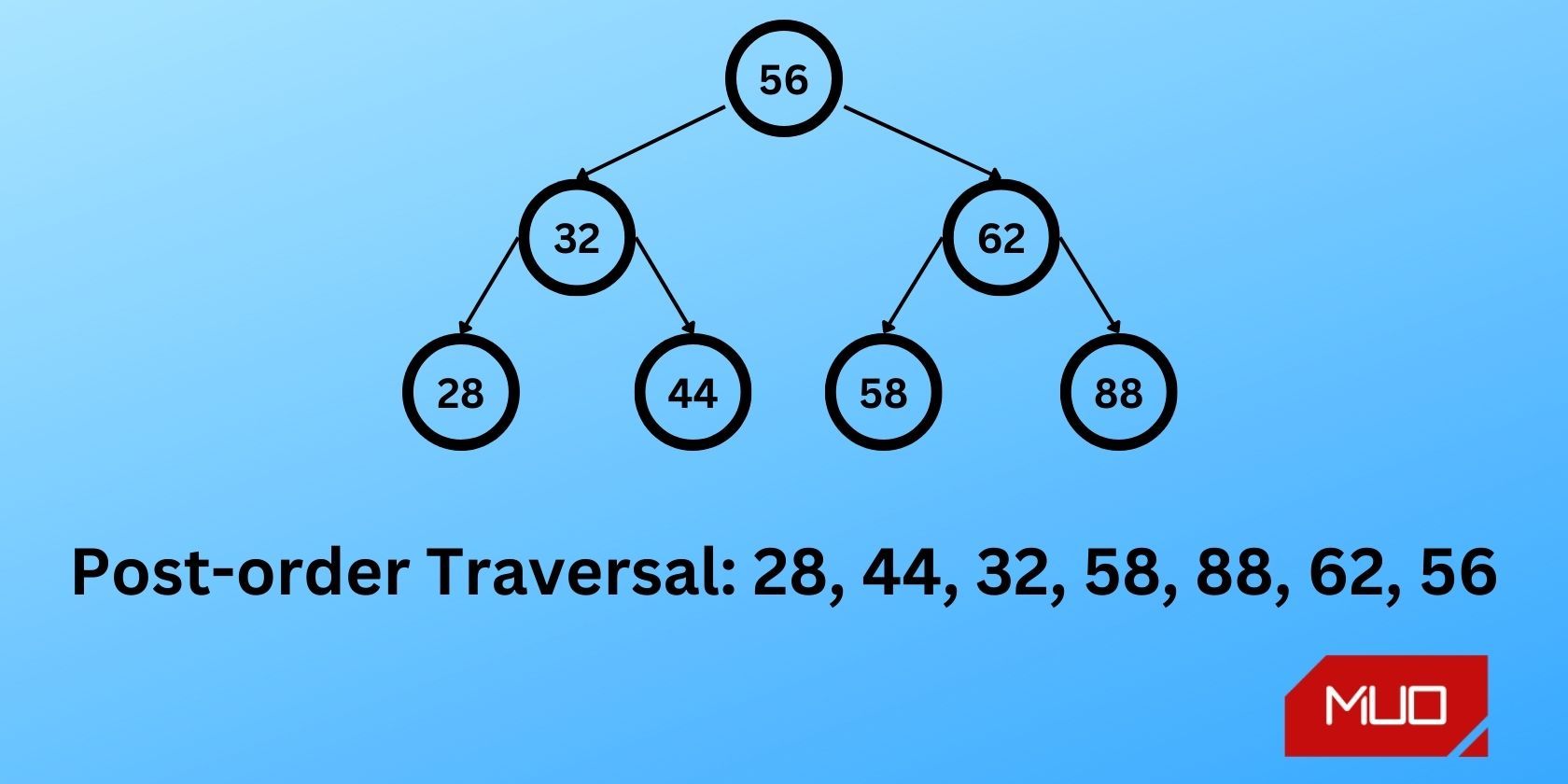
Since it processes the root node after both subtrees, this method it is called postorder traversal.
Finish by processing the root node, 56.
To process the subtree, rooted at 32, traverse its left subtree, 28.
Since 28 doesn’t have any children, move to the right subtree, 44.
Process 44 since it also has no children.
Lastly, process the root node, 32.
You’ve traversed this subtree in the order 28 -> 44 -> 32.
Process the right subtree using the same approach to visit nodes in the order 58 -> 88 62.
Finally, process the root node, 56. you could also use it to find the postfix expression of an expression tree.
The size of the binary tree is equal to the number of nodes in that tree.
It is crucial for a programmer to be well versed in algorithms.